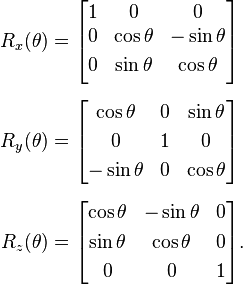NCF参数化建筑论坛

标题: 科普：旋转 [打印本页]

作者: panhao1 时间: 2010-10-30 14:35
标题: 科普：旋转
空间变换可以通过向量或是矩阵来完成一般多为3*3 或是4*4矩阵很容易获知一些基本变换的矩阵（来自精品课程的网站）

作者: panhao1 时间: 2010-10-30 14:36
本帖最后由 panhao1 于 2010-10-30 14:48 编辑 这里具体说下旋转 Rotation （引用wiki）Basic rotationsThere are three basic rotation matrices in three dimensions:

这里是绕xyz的旋转形式由此推知空间任意向量（轴）旋转的矩阵可以通过绕xyz轴旋转两次而推得 The orthogonal matrix (post-multiplying a column vector) corresponding to a clockwise/rotation with Euler angles φ,θ,ψ, with x-y-z convention, is given by:

这里的 φ,θ,ψ是向量（轴）与 xyz轴的夹角 Rotation matrix given an axis and an angleFor some applications, it is helpful to be able to make a rotation with a given axis. Given a unit vector u = (ux, uy, uz), where ux2 + uy2 + uz2 = 1, the matrix for a rotation by an angle of θ about an axis in the direction of u is

这个是更加一般的形式如果给出的条件是向量的坐标而不是夹角的话~~

作者: panhao1 时间: 2010-10-30 15:02
本帖最后由 panhao1 于 2010-10-31 05:26 编辑 最后就是绕空间任意线段旋转的问题其实有了Rodrigues旋转公式：

或是矩阵形式

就很清楚了那么就是把物体先平移到原点——旋转——然后平移回来就可以完成这里矩阵我就不推导了其实大家看完一二楼的内容应该很明白其实实际计算向量的时候只要M.r+Q

+Q Q为旋转轴的起点（point3d）公式中v是法向量（旋转轴） r就是要旋转的点P -Q形成的向量玩过DX9的应该看过下面的转自 http://hi.baidu.com/guigangsky/blog/item/7ad064a72e92a990d04358ff.html

第五章矩阵变换

一：为什么使用4×4矩阵？ 在3D中进行编程时，使用的是4×4矩阵来进行矩阵变换。初学者往往认为既然是三维空间，为何不使用3×3的矩阵来表示呢？这是因为3×3的矩阵不能表示有些变换，比如比如平移、投影、反射，因此，增大到4×4，这样，就可以描述更多的变换了。但是矩阵变成了4×4，为了做向量与矩阵的相乘，所以需要把向量增加为1×4，因为1×3的行矩阵和4×4的矩阵是无法相乘的；那么，如何使用第四个成员（用w来表示）呢？当把一个点放置到一个1×4的行矩阵中时，设置w=1,表示可以对点进行适当的平移,如果w=0,表示不可以对向量进行平移。比如：把点p = (1, 2, 3)放置到一个行向量中就象这样[1, 2, 3, 1]，同样把向量v = (21, 32, 33) 放置到一个行向量中就象这样[21, 32, 33, 0]； 二、矩阵平移 对图形进行平行移动是最基本的操作：

使用下面的矩阵可以把向量(x, y, z, 1)沿x轴移动px个单位，沿y轴移动py个单位，沿z轴移动pz个单位：

以下代码为设置一个向量，对它应用一个平移变换后，得到新的向量，完整的代码参见程序： private void button1_Click(object sender, System.EventArgs e)

{

Clear();

//定义一个测试的向量；

Vector3 myVect=new Vector3(3,6,8);

//用此向量来保存后来的结果；

Vector4 resultVect =new Vector4();

//生成一个平移矩阵，XYZ方向均增加4个单位

Matrix MatrixA=Matrix.Translation(4,4,4);

//对向量应用平移变换；

resultVect=Vector3.Transform(myVect,MatrixA);

//将返回的向量显示出来；

label9.Text =resultVect.ToString();

//将矩阵也显示出来；

DisplayMatrix(MatrixA,label1);

}

程序执行结果，执行程序，点击按钮，执行结果如下：

下面应用一个具体的实例： 1：新建一个工程，生成一个XOZ水平面（代码略）： 2：定义二个Mesh对象：Mesh mesh1=null，mesh2=null; 3：在图形的初始化函数中对它进行实例化，在这里是生成两个半径一样大小的小球： public bool InitializeGraphics() { …… mesh1=Mesh.Sphere(device,0.5f,20,20); mesh2=Mesh.Sphere(device,0.5f,20,20); ……. } 4:在渲染场景函数里：一个小球进行平移变换，另一个则不进行任何变换： private void Render()

{

if (device == null) return;

device.Clear(ClearFlags.Target, System.Drawing.Color.Black , 1.0f, 0);

SetupCamera();

device.BeginScene();

displayPlane();

device.Transform.World=Matrix.Translation(10,0,0);

mesh1.DrawSubset(0);

device.Transform.World=Matrix.Identity;

mesh2.DrawSubset(0);

device.EndScene();

device.Present();

} 程序执行结果如下：

三、矩阵旋转 如果对一个图形绕一个固定点或一条线进行旋转，结果示意如下：

图9

下面的矩阵把一个向量围绕x,y 和z轴旋转一个角度。注意这里应当为弧度值，当俯视绕轴原点时，角度是指顺时针方向的角度。

示例一：下面测试一向量应用旋转变换后的结果： private void button2_Click(object sender, System.EventArgs e)

{

Clear();

Vector3 myVect=new Vector3(3,6,8); Vector4 resultVect =new Vector4(); Matrix MatrixA=Matrix.RotationX((float)Math.PI/2);

resultVect=Vector3.Transform(myVect,MatrixA);

label9.Text =resultVect.ToString();

DisplayMatrix(MatrixA,label1);

} 在这里，我们是让此向量绕X轴旋转90度，可以想像成直线OA绕X轴旋转90度，得到直线OB，B点值即为所求向量值；执行结果如下：

示例二：下面应用一个具体的实例： 1：新建一个工程，生成一个XOZ水平面（代码略）： 2：定义二个Mesh对象：Mesh mesh1=null，mesh2=null; 3：在图形的初始化函数中对它进行实例化，在这里是生成两个长方体： public bool InitializeGraphics() { …… mesh1=Mesh.Box(device,0.5f,0.5f,16); mesh2=Mesh.Box(device,0.5f,0.5f,16); …… } 4:在渲染场景函数里：对一个长方体绕X轴旋转45度，另一个长方体则在原点绘出： private void Render()

{

……

device.Transform.World=Matrix.RotationX((float)Math.PI/4);

mesh1.DrawSubset(0);

device.Transform.World=Matrix.Identity;

mesh2.DrawSubset(0);

……

} 程序执行结果如下：

以上介绍的是绕X轴旋转，绕Y，Z轴旋转类似，矩阵是：

四、矩阵缩放 对物体进行缩放的示意图如下：

下面的矩阵即为把向量沿x轴缩放qx个单位，沿y轴缩放qy个单位，沿z轴缩放qz个单位：

注意，如果在每个方向上的值大于1为放大，小于1则为缩小；示例一： private void button3_Click_1(object sender, System.EventArgs e)

{

Clear();

Vector3 myVect=new Vector3(3,6,8); Vector4 resultVect =new Vector4();

Matrix MatrixA=Matrix.Scaling(2,0.5f,0.5F);

resultVect=Vector3.Transform(myVect,MatrixA);

label9.Text =resultVect.ToString();

DisplayMatrix(MatrixA,label1);

} 代码中，将向量X方向扩大为2倍，Y和Z方向分别缩小为2倍；得到结果向量值为：

示例二：以下代码将前面创建的两个长方体其中一个应用缩放变换，其中在X，Y方向上放大为原来的2倍，Z方向上缩小为原来的2倍，相关代码如下： …… device.Transform.World=Matrix.Scaling(2,2,0.5f)*Matrix.RotationX((float)Math.PI/4);

mesh1.DrawSubset(0);

device.Transform.World=Matrix.Identity;

mesh2.DrawSubset(0); …… 程序执行结果如下：

五、组合变换 一般情况下，需要对向量进行一系列的变换。比如，前面显示的长方体，为了不使两者叠在一起，先进行了缩放，再进行了旋转，其实还可以再应用其它变换，比如平移；假设把向量p = [5, 0, 0, 1] 在所有轴上缩小为原来的1/5，然后沿着y轴旋转π/4，最后把它在x轴上移动1个单位，在y轴上移动2个单位，在z轴上移动3个单位。设缩放、旋转、移动的变换矩阵分别是S, Ry, T，如下：

因此：

这样就得到了最后的结果，另一种简便的方法是通过使用矩阵相乘把3个变换矩阵合成一个矩阵。注意次序不要颠倒，否则结果会不一样。

那么 pQ = [1.707, 2, –3.707, 1]。和第一种方法得到的结果是一样的； 六、其它常用变换 有两个矩阵，常常用来设置场影及摄像机： 1：device.Transform.Projection用来获取或者设置投影变换矩阵，它本身也是一个Matrix型的变量。 2：Matrix.PerspectiveFovLH方法： public static Matrix PerspectiveFovLH( float fieldOfViewY, //Y方向的视觉范围，弧度表示，即Y方向的视域角 float aspectRatio, //视觉范围的长宽比 float znearPlane, //近裁剪平面 float zfarPlane//远裁剪平面 ); 定义长宽比的作用是，如果用户改变了窗口的大小，那么仍然就可以正确的显示物体的大小。最后两个参数是远及近裁剪平面，必须为这两个平面指定2个Z值，一般来说，假设物体将在Z轴的1.0f和1000f之间运动时，就分别把这两个参数设为1.0f，1000.0f。 3：Matrix.LookAtLH方法。在使用观察矩阵来建立一个立体的照相机模型后，需要设置不同的观察点，可以使用这种方法来设置相机。 public static Matrix LookAtLH( Vector3 cameraPosition,//相机位置 Vector3 cameraTarget, //相机的方向 Vector3 cameraUpVector //相机的Up向量 ); 其中第二个参数为相机的面对方向，假设相机面对的是Z轴的方向，那么就设置为(0,0,1)。

作者: miaomiao 时间: 2010-10-30 18:38
无语。。。。。。。。。。。。。

作者: njyqqq 时间: 2010-10-30 19:36
超级无语{:3_56:}

作者: 136595750 时间: 2010-10-30 20:54
目前不能理解。。。纠结

作者: tira 时间: 2010-10-30 21:22
顶~这个太有用了！

作者: zhouningyi1 时间: 2010-10-30 22:20
思路是不错的特别是3轴方向只要沿2轴旋转就可以到任意角度但具体应用？

作者: Swow 时间: 2010-10-30 22:48
支持了!精品课程网站是?

作者: stratagem 时间: 2010-10-30 23:21
能不能遍个vb后c+然后定义一个gh命令那样用起来会很方便

作者: claudemit 时间: 2010-10-31 00:02
rs里面矩阵变换那一块我用过单感觉当时和我想象的总有出入，没怎么明白 processing立面的popmartix和pushmatrix都是用这原理吧在看看研究下感谢科普

作者: panhao1 时间: 2010-10-31 05:16
12# claudemit 犀牛 maya SU 3d 的API里面都有矩阵变换的类犀牛的是最完善的（也包括曲面计算式最完善的）但是像processing里面就没有这类东西的自己写其实我之前发过matrix相关的类的代码不过有些人可能不大会用这里把用法介绍给大家

作者: panhao1 时间: 2010-10-31 05:20
8# zhouningyi1 我想我说的已经够清楚了公式的变量都注明了就差一个矩阵的行列式没有写了如果还不清楚可以看看线性代数这个好像是做openGL的基础吧

作者: zhouningyi1 时间: 2010-10-31 10:05
从理论到实践还是有一定距离的吧。。比如我觉得正12面体或者正20面体，可以确定了一个面心（边界点也行）以后，其他面心由旋转得到，我觉得那么好的对称性，其旋转矩阵应该有所规律。但看了这些公式心里还是没底的..

8# zhouningyi1 我想我说的已经够清楚了公式的变量都注明了就差一个矩阵的行列式没有写了如果还不清楚可以看看线性代数这个好像是做openGL的基础吧 panhao1 发表于 2010-10-31 05:20

登录/注册后可看大图

作者: samooo 时间: 2010-10-31 10:57
学习一下哦，呵呵

作者: grchitect 时间: 2010-10-31 13:22
看的头有点晕

作者: caijieteng 时间: 2010-10-31 14:49
多谢分享。。。。

作者: goodsky2009 时间: 2010-10-31 19:49
这貌似是计算机图形学的内容

作者: arvin1018 时间: 2010-10-31 21:42
這個東西很有用~~~有時間在研究

作者: jasonbb88 时间: 2010-11-1 02:59
楼主你是在华南理工大学读研吗？

作者: sharkliang 时间: 2010-11-3 17:50
矩阵变换那一块我用过单感觉当时和我想象的总有出入，没怎么明白

作者: panhao1 时间: 2010-11-9 03:26
21# jasonbb88 华科大4

作者: 沈高 时间: 2011-3-27 14:42
{:3_57:}矩阵都没学过，郁闷

作者: ddrddrblueworm 时间: 2011-4-2 19:27
非常，非常的不理解，是不是因为只学了办调子的高数啊

作者: ping88 时间: 2011-4-27 01:26
好的饿 3

作者: ping88 时间: 2011-4-27 01:35
好的 3

作者: 守约 时间: 2011-7-1 15:51
真是……高深{:3_50:}

作者: www.yyssf.com 时间: 2011-8-20 03:00
大家好我是新来的请大家多关照啊

作者: www.cchhee.com 时间: 2011-8-21 15:36
大家好我是新来的请大家多关照啊

作者: xiangzai 时间: 2011-9-9 12:13
我晕！！！！！！

作者: tingting87 时间: 2011-10-12 08:48
帮顶，谢谢楼主~

作者: 清90821 时间: 2012-2-16 08:35
果然很科普，暂时看不懂~顶个

作者: benemorphy 时间: 2012-3-3 17:04
很好的科普，支持！

作者: nevana 时间: 2012-7-2 18:39
扫盲了。。。学习学习

作者: porther 时间: 2012-8-6 08:12
建筑生成的基础之一，有用。

欢迎光临 NCF参数化建筑论坛 (http://ncf-china.com/)